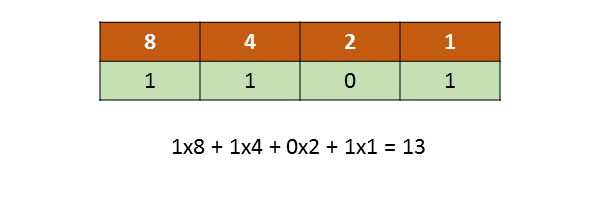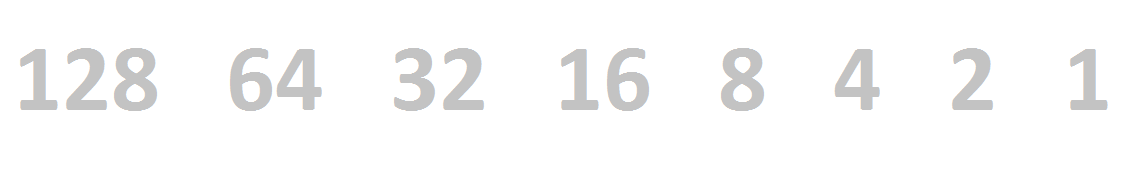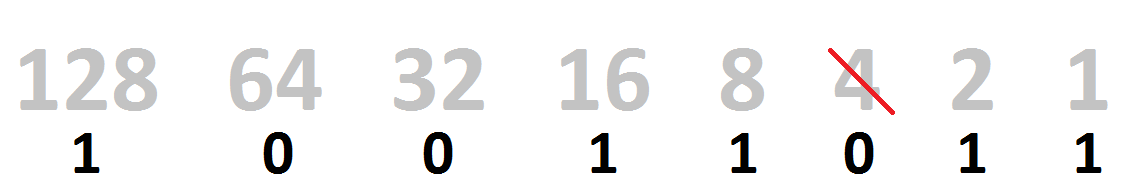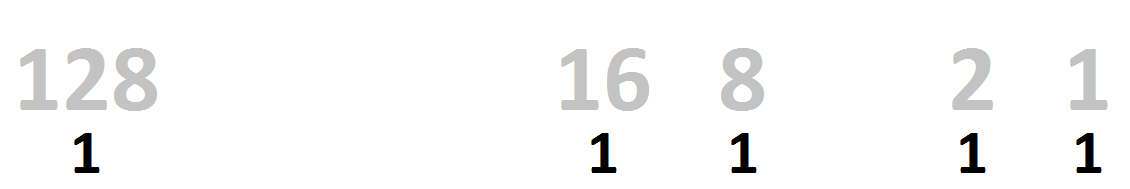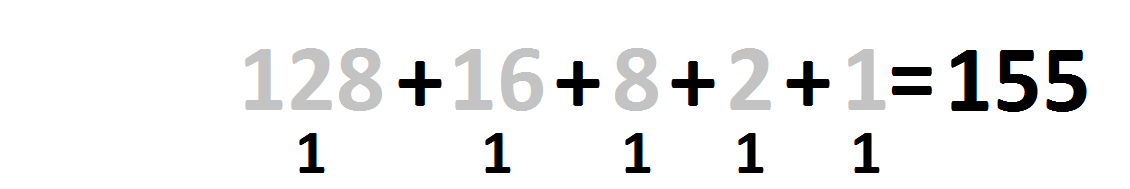The Binary number system

1111 is a binary number and 1111 is equal to 15. Another binary number is 1000 0001 which is equal to 129. But how is this? Well it is all because of "place values".
The denary number 3140 is said as "three thousand, one hundred and forty" because of where the 3, 1, 4  and 0 are placed.
  • There is a 3 in the place value "thousands"
  • 1 in the place value "hundreds"
  • 4 in the place value "tens"
  • and zero in the place value units.
When we are taught this denary number system at school, after a while we forget about the place values and we certainly do not write them down.
Binary has place values too, just different ones. The place value on the right side is not called "units", it is called 1. Going left, 1 is doubled and is 2. Going left again, 2 is doubled and the place value is 4. This repeats.
  • So, the binary number 0000 is equal to 0 denary because none of the place values are switched on (all zeros)
  • the binary number 0001 is equal to 1 denary because only the the place  value 1 is switched on
  • the binary number 0010 is equal to 2 denary because only the the place  value 2 is switched on
  • the binary number 0011 is equal to 3 denary because the the place  values for 1 and 2  is switched on (1+2=3)

Below, 1101 is equal to 13 because those place values are switched on and added together.
Finally, just like denary wee all stop writing the place values and are able to identify that binary 1001 is equal to.......?

8-bit binary

Binary using 4 places is called a nibble. Binary using 8 places is called a byte. Converting a byte to denary is the same as converting a nibble to denary.

Units of size for information or storage

Picture
Units of information

The binary game




​<-----Click here then choose "age 13"